Rubber Band Elastic Hysteresis Introduction

Modeling Rubber Band Cords Beyond Hooke's Law

There is a great deal of fun to be had with scale model "Bungee Jumping" activities using chains of rubber bands as the bungee cord. Often the accompanying discussion simplifies the treatment of the elasticity of the cord, using Hooke's law as an idealization. On such educational simulation and accompanying materials can be found at https://www.compadre.org/osp/items/detail.cfm?ID=13284.

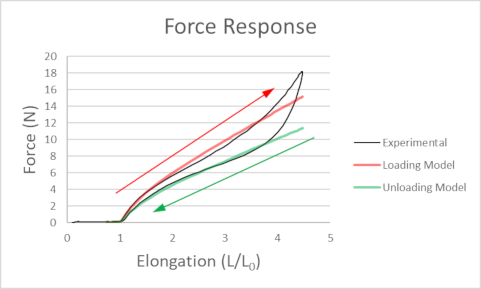
Real rubberbands offer an opportunity to explore topics like non-linear forces, energy loss and even elastic hysteresis. In the graph below shows the measured force response of a rubberband slowly stretched to almost five times its original length (the loading process) and then allowed to slowly relax to it's original length. Idealized force models are also shown for both the loading process (Loading Model) and the unloading process (Unloading Model). The idealized loading (red) and unloading (green) responses are of the form F_L,U(L)=K_L,U (L/L₀-(L₀/L)²), where the two constants K_L and K_U are for the loading (from completely relaxed) and (asymptotic) unloading from large elongation (L/L₀). The force-distance loop is traversed clockwise, and necessarily some work was done on the rubber band. This is part of the mechanism by which the bungee jumper looses energy during successive bounces, gradually coming to rest.

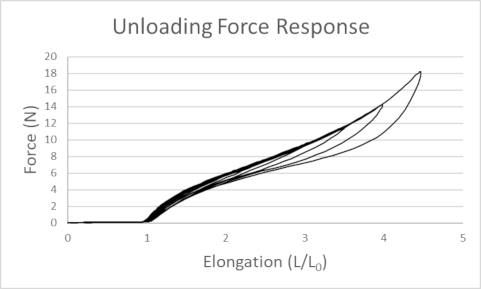
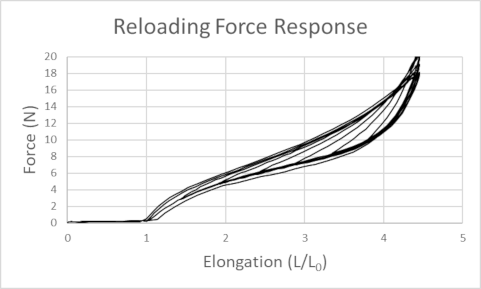
The following two experimental graphs show in more detail how a rubberband can respond to various loading and unloading scenarious. In the first graph below the band is loaded (stretched) to different levels and then allowed to completely relax (the band is compeltely unloaded) from , providing some insight into the band's general unloading force response. In the second graph the band was stretched to a set maximum length (for this series), then was partially unloaded before being reloaded to the maximum elongation, providing insight into the band's general reloading force response.

unloading force response of a rubberband

reloading force response of a rubber band

The simulation assumes that the force response will always fall between the idealized loading and unloading models. If the band is in a given force/elongation state and is unloaded, the response should parallel the family of curves in the Unloading Force Response graph. If the band is in a given force/elongation state and is loaded, the response should parallel the family of curves in the Reloading Force Response graph.

To mimic the behaviour for an unloading process from a set force/elongation state F_i, L_i the force excess above the idealized unloading model is modeled by a power law. Similarly, for the behaviour for a loading process from a set force/elongation state F_i, L_i the force deficit below the idealized loading model is also modeled by a power law. Both models can be written (choosing ± for the loading vs. unloading processes):
F(L,L_i,F_i) = F_U,L(L) +(F_i- F_U,L(L_i))|(L-L₀)/(L_i-L₀)|^p_U,L

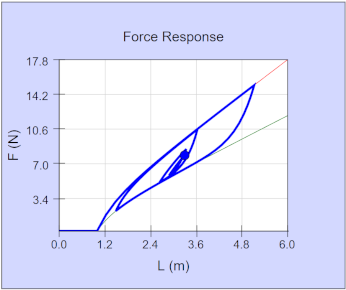
For loading, p_L = -2, so that the force deficit from the idealized model decreases rapidly for increasing length L, while p_U = 10 so that the force excess decreases very rapidly for decreasing length L. The firure below shows for force history for a "jump" where the weiight of the "jumper" stretched the cord to a maximum length of approximately 5 times the unstretched lenght of the band.