Introduction
There is a great deal
of fun to be had with scale model "Bungee Jumping" activities using
chains of rubber bands as the bungee cord. Often the
accompanying
discussion simplifies the treatment of the elasticity of the cord,
using Hooke's law as an idealization. On such educational
simulation and accompanying materials can be found at https://www.compadre.org/osp/items/detail.cfm?ID=13284.
This model explores energy loss and non linear forces that can affect the dynamics in a typical activity.
Basic parameters
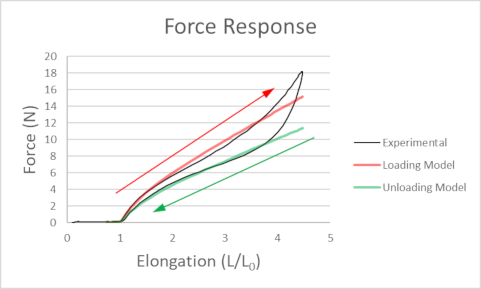
In this model, a few simple parameteers are used to characterize the rubber band properties: the band's unstretched length L0 (no tension) and two forces FL2x and FU2x. FL2x is the tension required to double the unstretched length (L = 2L0
) of the cord from a completely relaxed state, while FU2x is
the tension when the cord returns to double the unstretched length when
allowing the cord to relax from a greatly elongated state (L > 4*L0).
The force response when stretching (loading) the cord from
zero tension to about4.5 times its unstretched length then allowing the
cored to completely relax would typically look like the graph below.
The
only additional physical parameter needed for the simulation is the
mass of the jumper.
A few considerations:
- This model assumes the band
has been "broken in" by repeatedly stretching it
to at least the maximum length the cord will reach during a
bungee drop, aftr which the force response of a band is fairly
consistent over that range of elongation.
- A jumper mass whose weight is equal to FL2x will result in a first drop that stretches the cord to about 4L0.
- If you set FU2x = FL2x, there is no energy loss and if you set FU2x > FL2x, you get some unphysical energy production (think "flubber").
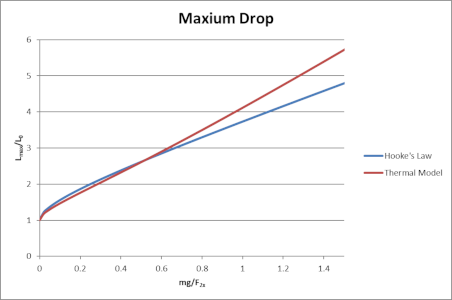
- For help in selecting an appropriate jumper mass for a given cord, the chart below was created from work and energy considerations.