The reduction of X-ray intensity due to absorbtion follows the following exponential decay:
I = I0 exp(-μt)
where I is the incident intensity, I0 is the transmitted intensity, μ is the absorption coefficient, and t is the thickness of the matterial. the mass absorption coefficient
μm = μ/ρ
is usually used in place of μ and a mass thickness
x=ρt
used in place of the physical thickness of the attenuating material.
Over the range of X-ray energies found in a typical diagnostic X-rays, μm is dominated by contributions from the phtoelectric effect (τm) and the Compton effect (σCm):
μm = τm+σCm
According to both reference 2 and 3, τm is proportional to the cube of atomic number Z and inversely proportional to the cube of the X-ray photon energy E. The behavior of σCm is less well defined. Both reference 2 and 3 note that σCm is independent of atomic number. Reference 2 only states that σCm decreases with increasing energy while reference 3 suggests that it is inversely proportional to photon energy.
The simplified model for μ used in the applet is given by
μm=(τ0(Z/Z0)3(E0/E)3+σ0(E0/E))
where τ0 and σ0 are the contributions of the photoelectric effect and the Compton effect at the reference atomic number Z0 and reference photon energy E0. The following values are used
| Z0 | 20 |
| E0 | 100 keV |
| τ0 | 0.085 cm2/g |
| σ0 | 0.2 cm2/g |
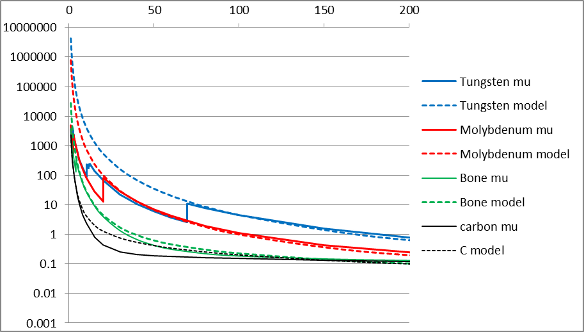
This discussion does not take into acount reduced interaction at lower energies due to insufficient X-ray photon enery to overcome the binding energy of the electrons (which produce the absorption edge features). As a result, the simple model used here will over estimate the photoelectric absorption of X-rays for higher Z materials at low to intermediate energies. While this model is inadequate for accurate modeling of X-ray interaction with matter, is is sufficiently accurate to provide the qualitative behaviour students will be exploring with this applet.
The graph below compares the simple model of μm with the
experimental data from reference 1: 
References:
(1) X-ray Mass Attentuation Coefficients, J. H. Hubbell and S. M. Seltzer , http://www.nist.gov/pml/data/xraycoef/
(2) Radiation oncology physics : a handbook for teachers and students
(3) Radiologic Science for Technologists, Stewart C. Bushong